Job Description Classification¶

Our mission¶
The mission is to automate job applications for everybody.
Pre-done work¶
I wrote a web-crawler in python to get job description from a German website called https://www.stepstone.de. I did the following steps:
- Crawling all the links pointing on sites that show job offers
- Crawling each job offer with all information available
- Job name
- Company and link to its description site
- Job type (part-time/full-time/freelance etc.)
- Description (Stepstone uses html-parts to divide each section of the job offer)
- Saving all of the divided descriptions in a DataFrame (pandas)
- 1st column: headline
- 2nd column: text
- Cleaning the data
- Reducing the labels from about 5000 to 5 so that we have the following labels:
- company: a description of the company ("About us"-page)
- tasks: a description of the job offered (especially the tasks of the job)
- profile: a description of the skills needed to fulfill the job's requirements ("Your profile")
- offer: a description of what the company offers for the applicant ("What to expect", "What we offer to you")
- contact: contact details for the applicant (also including a hint whom to adress in the application)
- Reducing the labels from about 5000 to 5 so that we have the following labels:
What this notebook covers¶
What we will do for this part, is to use the clean data to properly predict any part of a job offer to be one of the five categories. We will try to use machine learning algorithms to find specific patterns of the text to then match text to a label.
The data will be split into testing and training data and we will also pick a random text out of a random job offer to test our model on other data.
Investigating the dataset¶
Let's first see how the DataFrame looks like:
import pandas as pd
# save as originally imported
df_import = pd.read_csv("cleaned_classification_dataset.csv",index_col=0)
df_import.head(5)
Preprocessing¶
As we can see clearly, we have to do some preprocessing in order to be able to process the text we have. For that we will pick a list of random texts and build a function that properly tokenizes the text in order to compute it afterwards.
Make a list of 20 random 'documents'
documents = df_import["text"].tolist()
y = df_import["headline"].tolist() # y for later using these as labels
df_import["headline"].value_counts()
Remove the '\r's and '\n's
When crawling the data, I missed to remove these characters. No problem, we can solve this anyways. BUT we will not remove them. Instead, we will use them to implement a '\break\' which will tell our Tokenizer to make a new sentence out of the following. This is going to be useful for the POS Tagging procedure we will use.
new_documents = []
for doc in documents:
doc = doc.replace("\r","")
doc = doc.replace("\n","\\break\\")
new_doc = doc.split("\\break\\")
new_documents.append("")
for d in new_doc:
if d!=" " and d!="":
if d[-1]==" ":
d = d[:-1]
# replace unicodes
d = d.replace(u'\xa0', u' ')
d = d.replace(u'\xa4', u'ä')
d = d.replace(u'\xb6', u'ö')
d = d.replace(u'\xbc', u'ü')
d = d.replace(u'\xc4', u'Ä')
d = d.replace(u'\xd6', u'Ö')
d = d.replace(u'\xdc', u'Ü')
d = d.replace(u'\x9f', u'ß')
# Making everything to lower
d = d.lower()
new_documents[-1]+=d
lowercase_documents = new_documents
Removing all punctuations
sans_punctuation_documents = []
import string
for i in lowercase_documents:
sans_punctuation_documents.append(i.translate(str.maketrans('', '', string.punctuation)))
Modelling¶
Saving data for modelling
Now we save our newly made up documents to the X which we are going to use as data to train our model. We already defined the labels of the dataset, so we are ready to go.
X = sans_punctuation_documents
Making up the training function we will use to test the algorithms
We will split our data into training and testing datasets and then train it on that data.
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import MultinomialNB
from sklearn.pipeline import Pipeline
from sklearn.feature_extraction.text import TfidfTransformer
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.linear_model import SGDClassifier
from sklearn.model_selection import GridSearchCV
from pprint import pprint
from time import time
from sklearn.cross_validation import train_test_split
def train(classifier, X, y):
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=33)
classifier.fit(X_train, y_train)
print("Accuracy: {}".format(classifier.score(X_test, y_test)))
return classifier
Grid searching
Before using this function, we will perform a grid search on different parameters.
We will iterate through the following parameters:
- different pipelines
- at first, we will use the CountVectorizer and tfidf-transformer to preprocess and the Multinomial Naive Bayes Classifier
- Secondly, we'll try to use the Stochastic Gradient Descent Classifier to build the model based on the same preprocessing
- max_df of CountVectorizer
- When building the vocabulary, ignore terms that have a document frequency strictly higher than the given threshold (corpus-specific stop words)
- max_features of CountVectorizer
- If not None, build a vocabulary that only consider the top max_features ordered by term frequency across the corpus.
- n_gram_range of CountVectorizer
- The lower and upper boundary of the range of n-values for different n-grams to be extracted. All values of n such that min_n <= n <= max_n will be used.
- use_idf of TfIdfTransformer
- Enable inverse-document-frequency reweighting.
- smooth_idf of TfIdfTransformer
- Smooth idf weights by adding one to document frequencies, as if an extra document was seen containing every term in the collection exactly once. Prevents zero divisions.
- norm of TfIdfTransformer
- Norm used to normalize term vectors. None for no normalization.
- max_iter for SGDClassifier
- The maximum number of passes over the training data (aka epochs). It only impacts the behavior in the fit method, and not the partial_fit. Defaults to 5. Defaults to 1000 from 0.21, or if tol is not None.
- alpha for SGDClassifier
- Constant that multiplies the regularization term. Defaults to 0.0001 Also used to compute learning_rate when set to ‘optimal’.
- penalty for SGDClassifier
- The penalty (aka regularization term) to be used. Defaults to ‘l2’ which is the standard regularizer for linear SVM models. ‘l1’ and ‘elasticnet’ might bring sparsity to the model (feature selection) not achievable with ‘l2’.
We will bring an actual example to make clear how these parameters have an effect on the result.
Result of grid searching
We already iterated through all the parameters. That's why we only uncommented the parameters that were tested last. But let's see what parameters we get for a good fit.
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=33)
trial1 = Pipeline([
('vect', CountVectorizer()),
('tfidf', TfidfTransformer()),
('clf', MultinomialNB()),
])
trial2 = Pipeline([
('vect', CountVectorizer()),
('tfidf', TfidfTransformer()),
('clf', SGDClassifier(random_state=33)),
])
parameters = {
'vect__max_df': (0.5, 0.75, 1.0),
# 'vect__max_features': (None, 5000, 10000, 50000),
'vect__ngram_range': ((1, 1), (1, 2)), # unigrams or bigrams
# 'tfidf__use_idf': (True, False),
#'tfidf__smooth_idf': (True,False),
# 'tfidf__norm': ('l1', 'l2'),
'clf__max_iter': (5,),
'clf__alpha': (0.00001, 0.000001),
'clf__penalty': ('l2', 'elasticnet'),
}
grid_search = GridSearchCV(trial2, parameters, cv=5,
n_jobs=-1, verbose=1)
print("Performing grid search...")
print("pipeline:", [name for name, _ in trial2.steps])
print("parameters:")
pprint(parameters)
t0 = time()
grid_search.fit(X_train, y_train)
print("done in %0.3fs" % (time() - t0))
print()
print("Best score: %0.3f" % grid_search.best_score_)
print("Best parameters set:")
best_parameters = grid_search.best_estimator_.get_params()
for param_name in sorted(parameters.keys()):
print("\t%s: %r" % (param_name, best_parameters[param_name]))
train(grid_search.best_estimator_, X, y)
Result of model building
Very nice... Seems like we have a winners for the best fitting parameters:
Best score: 0.950
Best parameters set:
clf__alpha: 1e-05
clf__max_iter: 5
clf__penalty: 'l2'
vect__max_df: 1.0
vect__ngram_range: (1, 2)
So let's use the pipeline again to save the best classifier as 'clf'.
best_pipeline = Pipeline([
('vect', CountVectorizer(ngram_range=(1,2),max_df=1.0)),
('tfidf', TfidfTransformer(norm="l2")),
('clf', SGDClassifier(alpha=1e-05,max_iter=5,penalty='l2'))
])
clf = train(best_pipeline, X, y)
Quick testing the model¶
Proving the readiness of the model by a few examples
Now, we want to see some results. I used a few examples I just copied out of different parts of job offers. Just to show, how good our model is, let's test them out:
docs_new = [
"Es erwartet Sie eine abwechslungsreiche Tätigkeit in einem international ausgerichteten Konzern. Vom ersten Tag an werden Sie bei SAINT-GOBAIN von einem kollegialen Team aufgenommen und unterstützt. Sie erhalten bei SAINT-GOBAIN eine gründliche Einarbeitung in Ihr Aufgabengebiet und lernen die Arbeitsmethodik eines komplexen Konzerncontrollings kennen.Leidenschaft, Inspiration, Teamgeist, Innovation und Werte sind bei uns keine bloßen Worthülsen. Sie werden gelebt!",
"Sie haben die Fachoberschulreife oder das Abitur mit guten Ergebnissen abgeschlossen Sie haben Spaß an kaufmännischen Themen und Lust darauf, Einblick in viele unterschiedliche Arbeitsfelder eines Industrieunternehmens zu erhalten Erste Erfahrungen in MS Office wie Word und Excel sind wünschenswert Sie arbeiten gerne im Team und sind kommunikativ Sie sind verantwortungsbewusst, engagierte und haben eine gute Auffassungsgabe",
"Neben einem erfolgreich abgeschlossenen Bachelor-, Master- oder Diplomstudium konnten Sie bereits praktische Erfahrung in der Personal- und Organisationsentwicklung sammeln. Sie haben nachweisbare Schwerpunkte und erfolgreiche Projekte in mehreren, der oben genannten Themenschwerpunkten. Idealerweise verfügen Sie über eine Zusatzausbildung im Bereich Organisationsentwicklung, Change Management oder Coaching. Sie arbeiten zuverlässig und effizient, auch in einem dynamischen Umfeld mit ständig wechselnden Anforderungen. Ihre Beratungskompetenz sowie Ihre selbstständige und zielorientierte Arbeitsweise machen Sie zu einem starken Partner. Reisebereitschaft sowie sehr gute Deutsch- und Englischkenntnisse runden Ihr Profil ab. Bitte teilen Sie uns in Ihrer Bewerbung, falls vorhanden, Ihre Präferenz für einen Standort (Karlsruhe oder Montabaur) mit.",
"United Internet ist mit erfolgreichen Marken wie 1&1, GMX und WEB.DE der führende europäische Internet-Spezialist. Über 9.000 Mitarbeiter betreuen rund 57 Millionen Kunden-Accounts in 11 Ländern. Seit 1998 ist die United Internet AG an der Frankfurter Wertpapierbörse gelistet.",
"Interessiert? Wir freuen uns auf Ihre aussagefähige Bewerbung mit Angabe Ihrer Gehaltsvorstellung und Kennziffer: KA-SeHe-1810107. Details erfahren Sie unter www.united-internet.de oder telefonisch bei Jasmin Straßer: +49 721 91374-6216 ."
]
The prediction of these documents must look like the following to be considered correctly: [ 'offer', 'profile', 'profile', 'company', 'contact' ]
Predicting
clf.predict(docs_new)
Got it right!! OK, let's save our model so we can use it for further analysis in different programs. This is useful stuff!
Saving the model¶
We use pickle to store it in our filesystem. We can load it afterwards via the following command:
loaded_model = pickle.load(open(filename, 'rb'))
I will store this as 'anzeigen_model_95.sav' to be able reconstruct the model's accuracy afterwards.
#import pickle
#filename = 'anzeigen_model_95.sav'
#pickle.dump(clf, open(filename, 'wb'))
Inside the model¶
Let's see how the model was constructed. We used a pipeline which looks the following:
- preprocess ourselves (to remove the most obvious disorders in the data)
- we will not go deeper into this, because you could already follow each step
- Count-Vectorizing the data
- Using tf-idf to transform the data
- Building a model using the Stochastic Gradient Classifier
- also doing grid search to find the best parameters
Choosing data to perform the pipeline for deeper analysis¶
We want to use random passages from job offers to show how the preprocessing is done and how the classifier works on it. That's why we chose the data we already used for quick testing the model (docs_new). In addition, we made the preprocessing steps as for our main dataset:
preprossing_list = []
analysis_data = []
for doc in docs_new:
doc = doc.replace("\r","")
doc = doc.replace("\n","\\break\\")
new_doc = doc.split("\\break\\")
preprossing_list.append("")
for d in new_doc:
if d!=" " and d!="":
if d[-1]==" ":
d = d[:-1]
# replace unicodes
d = d.replace(u'\xa0', u' ')
d = d.replace(u'\xa4', u'ä')
d = d.replace(u'\xb6', u'ö')
d = d.replace(u'\xbc', u'ü')
d = d.replace(u'\xc4', u'Ä')
d = d.replace(u'\xd6', u'Ö')
d = d.replace(u'\xdc', u'Ü')
d = d.replace(u'\x9f', u'ß')
# Making everything to lower
d = d.lower()
preprossing_list[-1]+=d
analysis_data = preprossing_list
analysis_processed = []
for i in analysis_data:
analysis_processed.append(i.translate(str.maketrans('', '', string.punctuation)))
analysis_processed
That's how the text look like before we even use the CountVectorizer.
Count Vectorizing¶
OK, so the next step is to make a vector out of the text.
Paramaters
CountVectorizer() has certain parameters which take care of these steps for us. They are:
lowercase = TrueThe
lowercaseparameter has a default value ofTruewhich converts all of our text to its lower case form.
token_pattern = (?u)\\b\\w\\w+\\bThe
token_patternparameter has a default regular expression value of(?u)\\b\\w\\w+\\bwhich ignores all punctuation marks and treats them as delimiters, while accepting alphanumeric strings of length greater than or equal to 2, as individual tokens or words.
stop_wordsThe
stop_wordsparameter, which we will not use. We tried the version WITH stop_words but it didn't work as well as without. Stop words are the words in a sentence that very often appear and are not there to give us hints about the actual meaning of the test. BUT for this case, every word that is more or less used in specific parts of the job offer help us to gather information, so this time, we keep them.
You can take a look at all the parameter values of your count_vector object by simply printing out the object as follows:
count_vector = CountVectorizer()
count_vector
Fitting the vocabulary / Creating a bag of words
Here we'd like to introduce the Bag of Words(BoW) concept which is a term used to specify the problems that have a 'bag of words' or a collection of text data that needs to be worked with. The basic idea of BoW is to take a piece of text and count the frequency of the words in that text. It is important to note that the BoW concept treats each word individually and the order in which the words occur does not matter.
OK, good. Let's try to fit the CountVectorizer on our text data:
count_vector.fit(analysis_processed)
count_vector.get_feature_names()
This is like a dictionary on which you can classify specific documents. The CountVectorizer basically learned the vocabulary of all processed documents.
Frequency Matrix
You could also use the CountVectorizer to transform the text into a vector. The first sentence would look like this if you directly transformed it via CountVectorizer:
vectorized_docs = count_vector.transform(analysis_processed)
We want to show you a way to visualize the vectors:
frequency_matrix = pd.DataFrame(vectorized_docs.toarray(),
columns = count_vector.get_feature_names())
frequency_matrix
As you can see, the CountVectorizer takes the frequency of each word occuring in each document and puts it in the column labelled by the word. For our dataset, we got a very huge bag of words, which means a great number of columns and of course, rows as well...
Tf-idf¶
"Term frequency - inverse document frequency" is a great way to add weights to our vocabulary. Here is how Wikipedia describes tf-idf:
- term frequency–inverse document frequency, is a numerical statistic that is intended to reflect how important a word is to a document in a collection or corpus. It is often used as a weighting factor in searches of information retrieval, text mining, and user modeling. The tf–idf value increases proportionally to the number of times a word appears in the document and is offset by the number of documents in the corpus that contain the word, which helps to adjust for the fact that some words appear more frequently in general. Tf–idf is one of the most popular term-weighting schemes today; 83% of text-based recommender systems in digital libraries use tf–idf. (https://en.wikipedia.org/wiki/Tf%E2%80%93idf)
The method is the following. We have two parts:
Term frequency
${{tf} (t,d)=f_{t,d}}$
where: ${t}= $ the number of times that term t occurs in document ${d}$ If we denote the raw count by $f_{t,d}$.
Inverse document frequency
${{idf} (t,D) = { \log {\frac {N}{n_{t}}}}}$
where:
${t}= $ the number of times that term t occurs in all documents (corpus) ${D}$ If we denote the raw count by $f_{t,d}$
${N}= $ total number of documents in the corpus ${N} = {|D|}$.
- $n_{t} = $ number of documents where the term ${t}$ appears
Putting it together
${tfidf(t,d,D)=\mathrm {tf} (t,d)\cdot \mathrm {idf} (t,D)}$
This means we take into concern how many times a word is counted in our text (we did this already) and then weight the word regarding its uniqueness which we find out when we look at the other documents.
Using it for our example
We will transform our data which CountVectorizer already preprocessed for us:
transformer = TfidfTransformer()
transformed_docs = transformer.fit_transform(vectorized_docs)
tfidf_matrix = pd.DataFrame(transformed_docs.toarray(),
columns = count_vector.get_feature_names())
tfidf_matrix
We can see that for each occuring word in a document, we get a value finally creating a vector of each document which we can analyze more easily. In the following, we will see how the Stochastic Gradient works and how these vectors are used to categorize parts from job offers.
The Classifier¶
Stochastic gradient descent (often shortened to SGD), also known as incremental gradient descent, is an iterative method for optimizing a differentiable objective function, a stochastic approximation of gradient descent optimization. It is called stochastic because samples are selected randomly (or shuffled) instead of as a single group (as in standard gradient descent) or in the order they appear in the training set.
The classifier faces the following challenge:
Finding a way to match something like
array([0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0.12777782, 0. , 0.08557429, 0. ,
0. , 0. , 0. , 0.12777782, 0. ,
0. , 0. , 0. , 0.12777782, 0.12777782,
0.12777782, 0. , 0. , 0.30927101, 0. ,
0. , 0. , 0. , 0. , 0. ,
0.12777782, 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0.08557429, 0. ,
0. , 0. , 0.12777782, 0. , 0.17114859,
0.20618068, 0. , 0.10309034, 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0.10309034, 0. , 0.12777782,
0.12777782, 0.12777782, 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0.12777782, 0. , 0. , 0. ,
0. , 0.12777782, 0. , 0. , 0. ,
0. , 0.10309034, 0. , 0. , 0. ,
0.14397559, 0. , 0.12777782, 0.12777782, 0. ,
0.12777782, 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0.12777782, 0.12777782,
0. , 0.12777782, 0. , 0.12777782, 0. ,
0.12777782, 0.12777782, 0. , 0.12777782, 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0.25555563, 0. , 0. , 0. ,
0. , 0. , 0.28795117, 0.10309034, 0. ,
0. , 0. , 0. , 0. , 0. ,
0.12777782, 0.10309034, 0.12777782, 0. , 0. ,
0. , 0. , 0.12777782, 0. , 0.18266044,
0. , 0.08557429, 0. , 0. , 0.12777782,
0. , 0. , 0. , 0.12777782, 0.12777782,
0. , 0. , 0. , 0.25555563, 0.12777782,
0. , 0. , 0. , 0. , 0.12777782,
0. , 0. , 0. , 0. , 0. ,
0. , 0. ]
into a label (this case: offer)
sklearn provides an introduction about how the classifier works:
- Basic description: Linear classifiers (SVM, logistic regression, a.o.) with SGD training.
- This implementation works with data represented as dense or sparse arrays of floating point values for the features. The model it fits can be controlled with the loss parameter; by default, it fits a linear support vector machine (SVM). We are using the default loss parameter.
Support Vector Machines
By Larhmam - Own work, CC BY-SA 4.0, Link
So we want to classify the data we have transformed into vectors (as you can see above). A data point is viewed as a ${p}$ p-dimensional vector (a list of ${p}$ numbers, this case: 192-dimensional), and we want to know whether we can separate such points with a ${(p-1)}$-dimensional hyperplane.
Intuitively, a good separation is achieved by the hyperplane that has the largest distance to the nearest training-data point of any class (so-called functional margin), since in general the larger the margin the lower the generalization error of the classifier.
Our training set:
- $({\vec {x}}_{1},y_{1}),\,\ldots ,\,({\vec {x}}_{n},y_{n})$
One-vs.-rest - multilabel classification (https://en.wikipedia.org/wiki/Multiclass_classification#One-vs.-rest)
One-vs.-rest (or one-vs.-all, OvA or OvR, one-against-all, OAA) strategy involves training a single classifier per class, with the samples of that class as positive samples and all other samples as negatives. This strategy requires the base classifiers to produce a real-valued confidence score for its decision, rather than just a class label; discrete class labels alone can lead to ambiguities, where multiple classes are predicted for a single sample.
Measuring the training failure:
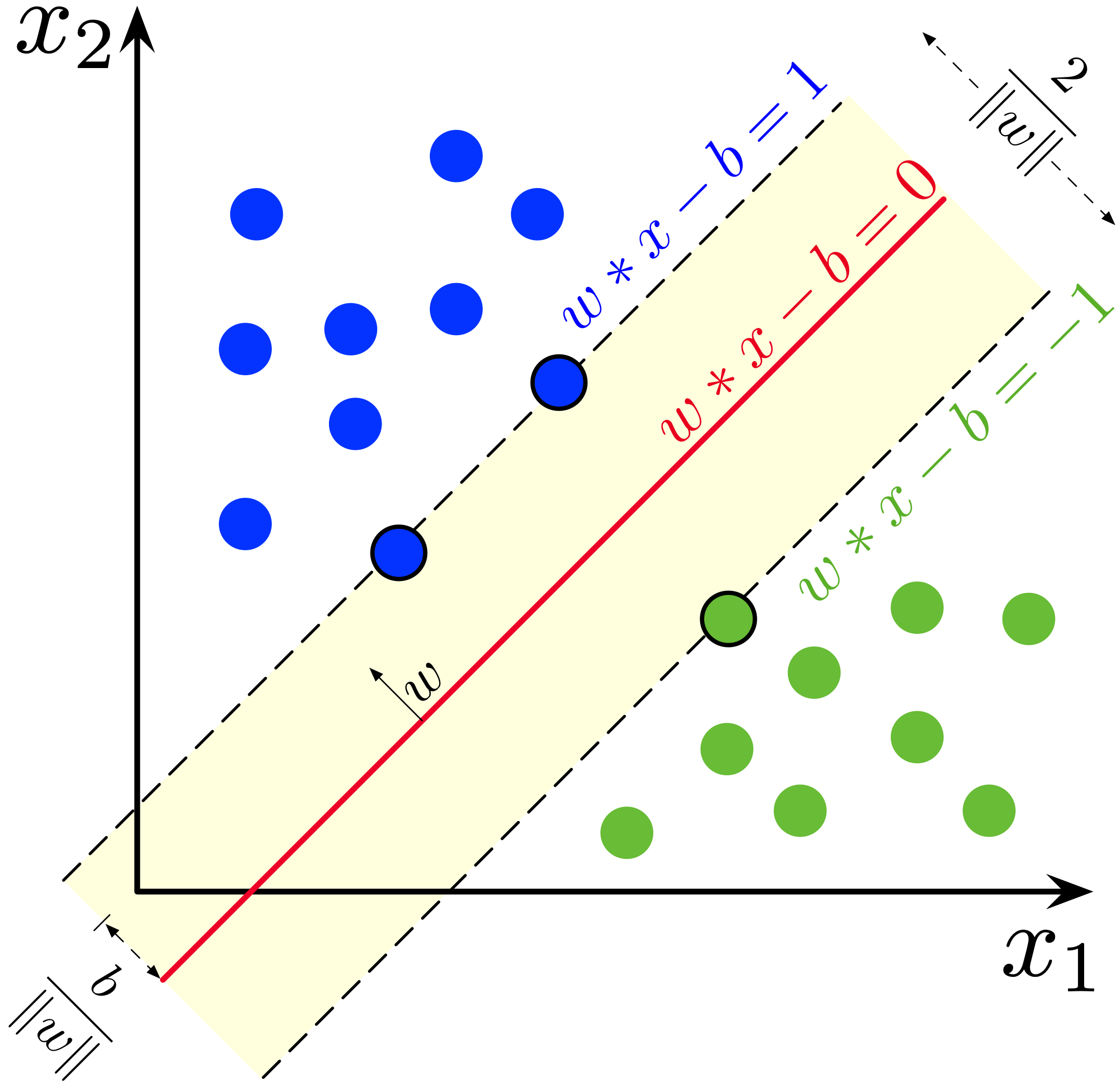
${y}_i = {w}^T {x}_i + {b}$ where you should think of ${w}$ and ${b}$ as representing a hyperplane, given by the points where ${w}^T · {x} + {b} = 0$. This hyperplane separates the data, and is known as the decision boundary.
So by putting each ${x}_i$-value into the classifier, we will get a score for each class:
${y}_{i1}$ = company
${y}_{i2}$ = offer
${y}_{i3}$ = profile
${y}_{i4}$ = tasks
${y}_{i5}$ = contact
m = number of data pairs
n = number of classes
So we formulate the loss - if the true category is company (${y}_{1}$) - the following way:
${L_i} = \sum_{j\neq1}^n{\max \left(0, y_{ij} - y_{i1} + 1 \right)}$
Hint: we take 5 as an input for the summarization because we have 5 categories!
The next step is to aggregate the loss and do that for each ${x_i}$ and then average the results. A you can see, as long as the value of the right prediction MINUS 1 is greater than all the other predictions for the other categories, we get a loss of zero, and that shall be our goal.
Our loss function also gets a regularization term attached so we prevent overfitting. This one is called penalty and we tested two different regularization-terms (l1 and l2) and finally picked l2 for our best predicting model:
${L} = \frac {1} {n} \sum_{i}^n \frac {1} {m} \sum_{j}^m {L_{ij}} + {R(W)}$
$R(w) = \frac{1}{2} \sum_{i=1}^{n} w_i^2$
=> https://scikit-learn.org/stable/modules/sgd.html#sgd
This way we add another value to our loss function to penalize high dimensional weights and incentify lower dimensional and more generalizing models.
Optimization: Stochastic Gradient Descent
We now want to minmize the error (loss) to have a good model. This is done by the following way:
$L_{i} = \sum_{j \neq y_{i}} max(0,w_{j}^{T}x_{i} - w_{y_{i}}^{T}x_{i} + \Delta)$
In order to obtain the gradient, we do the following differentiations:
$w \leftarrow w - \eta (\alpha \frac{\partial R(w)}{\partial w}+ \frac{\partial L(w^T x_i + b, y_i)}{\partial w})$
$\eta^{(t)} = \frac {1}{\alpha (t_0 + t)}$
where $\alpha = 0.000001$ (Grid Search found this parameter as best suited)
Stochastic gradient descent uses mini batches (samples) to get an estimate of the true gradient. This helps us to reduce cost in computing power and still get to the result we wish to have.
Summary
All in all, for each step the SVM gets a better result for the classification until the error/loss is minimized. In a very simplified way, this can look like the following:

By Joe pharos at the English language Wikipedia, CC BY-SA 3.0, Link
In the end, we get this beautifully labelled data when implementing this model. This is a great way to make crawling job descriptions easier and in the end to separate raw job descriptions inputted by the user in a way we can cope with more easily.